Blueprint 6: "The Processing Line" 🚶→🚶→🚶

1. The Mission Briefing: A Problem of Fairness

"Unlike the command spire, some tasks must be handled with absolute fairness, in the exact order they arrive. We can't let a low-priority task that arrived first be delayed by a high-priority task that arrived later. We need a 'First-In, First-Out' (FIFO) structure."

Imagine the ship's fabricator receiving a list of print jobs. If a request for a simple wrench arrives before a complex engine part, it should be printed first. If we process the last request first (like a Stack), our engineers will be waiting for simple tools while the fabricator is tied up with a long, complex job that was submitted later. This is inefficient and unfair. For this, we need a different kind of tool: the Queue.

2. The Analogy: A Line at a Ticket Counter

A Queue is exactly like a line of people waiting for a ticket.

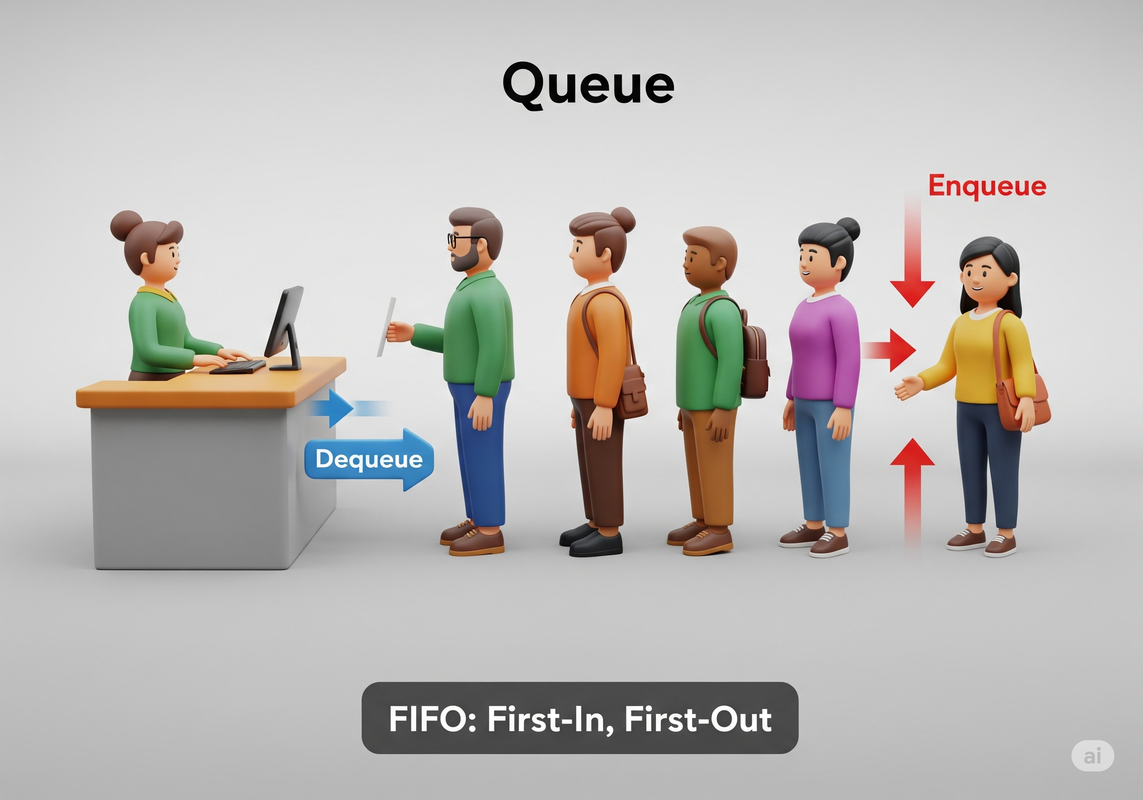
Illustration of people lining up for a ticket counter, demonstrating the FIFO principle.

The first person to get in line is the first person who gets to buy a ticket.
New people always join at the back of the line.
The person at the front of the line is always the next to be served.

This simple, fair, and intuitive process is the core of the Queue data structure. It guarantees that items are processed in the order of their arrival. This is the FIFO (First-In, First-Out) principle.

3. Visualizing the Operations

The two primary operations on a queue have special names that mirror the analogy:

Enqueue: Adding a new item to the rear (back) of the queue.
Dequeue: Removing the item from the front of the queue.

Interactive Queue (FIFO) Simulation

Visualize the First-In, First-Out principle of a queue.

Queue is empty

4. Implementing a Queue: The Blueprints

Like a Stack, a Queue is a conceptual rule that can be built using other data structures, most commonly a Linked List or an Array.

Method 1: Using a Linked List (The Truly Efficient Way)

A Linked List is a natural and highly efficient way to build a Queue. By keeping track of both the head and the tail of the list, we can achieve true O(1) performance for both of our main operations.

Enqueue: Add a new node to the tail (O(1)).
Dequeue: Remove the head node (O(1)).

Code Example: Linked-List-Based Queue

from collections import deque

# In Python, collections.deque is a highly optimized
# double-ended queue, perfect for both stack and queue implementations.
# It's implemented in C and is much faster than using a list for
# appends and pops from the left.

queue = deque()

# Enqueue
queue.append('a')
queue.append('b')

# Dequeue
item = queue.popleft() # item is 'a'

Method 2: Using an Array (The Simple, But Flawed Way)

You can also implement a Queue with a simple dynamic array. While enqueue (using the array's push method) is efficient (O(1) on average), dequeue is not. Removing an item from the front of an array (using a method like `shift()` or `pop(0)`) requires every other element to be shifted one position to the left, which is an O(n) operation. This can be a major performance bottleneck in large-scale systems.

5. An Important Optimization: The Circular Queue

When using an array, as you dequeue items, you leave empty, unused space at the beginning. A Circular Queue (or Ring Buffer) solves this.

The Analogy: Instead of a single line, imagine people waiting in a circle. When the person at the front is served, the "front" of the line simply moves to the next person in the circle, instead of everyone taking a step forward.

The Logic: It's an array with two pointers, `front` and `rear`. When a pointer reaches the end of the array, it "wraps around" to the beginning. This reuses the empty space and makes the array-based implementation much more efficient.

Circular Queue (Size 8)

Front

Rear

If we dequeue, `Front` moves to 5. If we enqueue, `Rear` wraps around to 0.

6. The Architect's Toolkit: Core Queue Operations

Method	Description	Analogy	Time Complexity
enqueue(item)	Adds an item to the rear of the queue.	Joining the back of the line.	O(1)
dequeue()	Removes and returns the front item.	Being served at the front.	O(1)
peek() / front()	Returns the front item without removing it.	Seeing who is next in line.	O(1)
isEmpty()	Returns true if the queue has no items.	Checking if the line is empty.	O(1)
size()	Returns the number of items in the queue.	Counting the people in line.	O(1)

7. Common Use Cases (In the Labyrinth and on Earth)

The FIFO principle of queues is essential for many systems:

Breadth-First Search (BFS): In graph and tree traversal, a queue is used to keep track of nodes to visit level by level. This is how you'll find the shortest path in the Labyrinth's star map.
Resource Management: Operating systems use queues for CPU scheduling, disk scheduling, and managing print jobs.
Buffering: When data is transferred between a fast process (like a network download) and a slow process (like writing to a disk), a queue acts as a buffer to hold the data so none is lost.

8. Blueprint Summary

Concepts Unlocked: Queues, FIFO (First-In, First-Out), enqueue, dequeue, peek, Linked-List-based implementation, the inefficiency of array-based queues, Circular Queues.