Blueprint 10: "The Priority Matrix" 🔼

Blueprint 10: "The Priority Matrix" 🔼

1. The Mission Briefing: A Problem of Priority

"Architect, a standard FIFO queue is fair but unintelligent. It can't distinguish between a critical 'Shield Failure' alert and a non-critical 'Cargo Report'. We need a structure that functions like a waiting list but always serves the most important item first, regardless of when it arrived."

In critical situations, we can't simply process tasks in the order they appear. We must handle the highest priority item immediately. This requires a specialized data structure that is always aware of the most important element it contains. This structure is known as a Priority Queue, and the most efficient way to build it is with a specialized tree called a Heap.

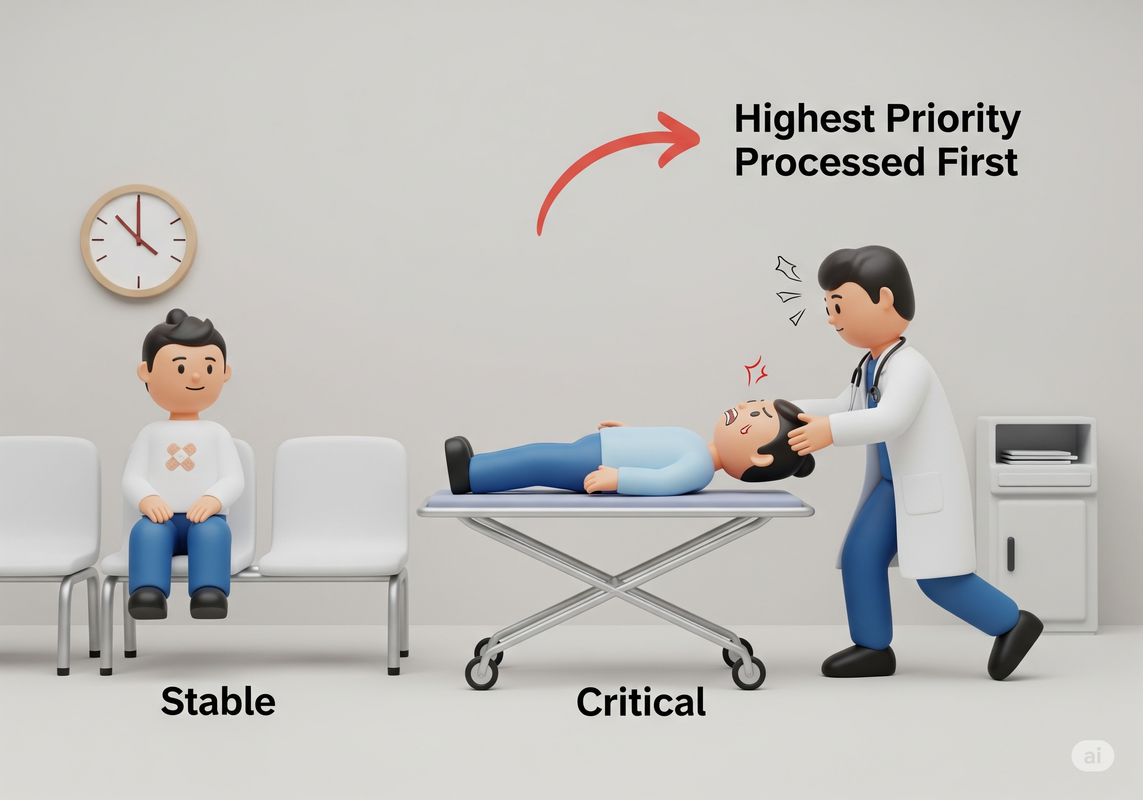
2. The Analogy: The Hospital Emergency Room

A Priority Queue is like an ER. Patients are not treated in the order they arrive (FIFO); they are treated based on the severity of their condition. A critical patient who just arrived will be seen before a stable patient who has been waiting for an hour. The Heap is the specialized tree structure we use to build this efficient system.

3. The Blueprint: What is a Heap?

A Heap is a special type of binary tree that must follow two strict rules to maintain its perfect order.

Rule #1: The Shape Property (It must be a Complete Binary Tree)

A heap must be a complete binary tree. This means all levels of the tree are completely filled, except possibly the last level, which is filled from left to right.

Rule #2: The Heap Property (The Parent-Child Order)

Every node in the heap must obey a specific rule regarding its value compared to its parent's value. There are two types:

• Max-Heap: The value of every parent node is greater than or equal to the value of its children. This means the largest element is always at the root.
• Min-Heap: The value of every parent node is less than or equal to the value of its children. This means the smallest element is always at the root.

This property is what guarantees that the highest (or lowest) priority item is always at the very top, ready for instant access (O(1) to peek).

4. The Implementation Secret: Heaps are Arrays!

While we visualize heaps as trees, we almost never implement them with traditional TreeNode objects and pointers. For maximum efficiency, a heap is stored as a simple Array.

We can do this because a complete binary tree has a very predictable structure. From any element at index i in the array, we can instantly calculate the index of its parent and children:

• Parent of i: floor((i - 1) / 2)
• Left Child of i: 2 * i + 1
• Right Child of i: 2 * i + 2

5. Keeping the Balance: The Heapify Operations

Adding or removing items takes O(log n) time because the heap needs to perform a re-balancing act to ensure the Heap Property is never violated.

A. insert (The "Bubble-Up" or "Heapify-Up" Operation)

When we add a new element, we place it at the first available spot (the end of the array) to maintain the "complete tree" shape. Then, we "bubble it up" by repeatedly swapping it with its parent until it's in a position that satisfies the heap property.

B. extractMax/Min (The "Bubble-Down" or "Heapify-Down" Operation)

To remove the root (the highest priority item), we can't just leave a hole. We take the last element in the heap, move it to the root's position, and then "bubble it down." We repeatedly swap it with its smaller (for a Min-Heap) or larger (for a Max-Heap) child until it settles into a position that satisfies the heap property.

6. Code Example: A Min-Heap Class in JavaScript/TypeScript

# Python's built-in 'heapq' module provides min-heap functionality.
import heapq

my_heap = []
heapq.heappush(my_heap, 10)
heapq.heappush(my_heap, 5)
heapq.heappush(my_heap, 20)

# Smallest item is always at index 0
# my_heap is now [5, 10, 20] (not necessarily sorted, but obeys heap property)

smallest = heapq.heappop(my_heap) # smallest is 5

7. Blueprint Summary

Concepts Unlocked: Priority Queues, Heaps (Max-Heap & Min-Heap), Complete Binary Tree Property, Heap Property, Array-based Heap Representation, Heapify (Bubble-Up & Bubble-Down), O(log n) insertion/deletion.