Blueprint 11: "The Galactic Network" 🕸️
Blueprint 11: "The Galactic Network" 🕸️
1. The Mission Briefing: The Interconnected Universe
"You've discovered the Labyrinth's true nature. It's not a line or a tree. It's a vast, interconnected network where any node can connect to any other node. This level of complexity requires a new data structure: the Graph."
The relationships we've modeled so far have had limitations. Arrays are linear, Linked Lists are chains, and Trees have a hierarchical structure. But what about relationships where direct connections can exist between any two entities, regardless of a hierarchy or sequence? Think of social networks, transportation systems, or the very neural network of a mind. These are best represented by Graphs.
2. The Analogy: The City Map
A Graph is like a city map.
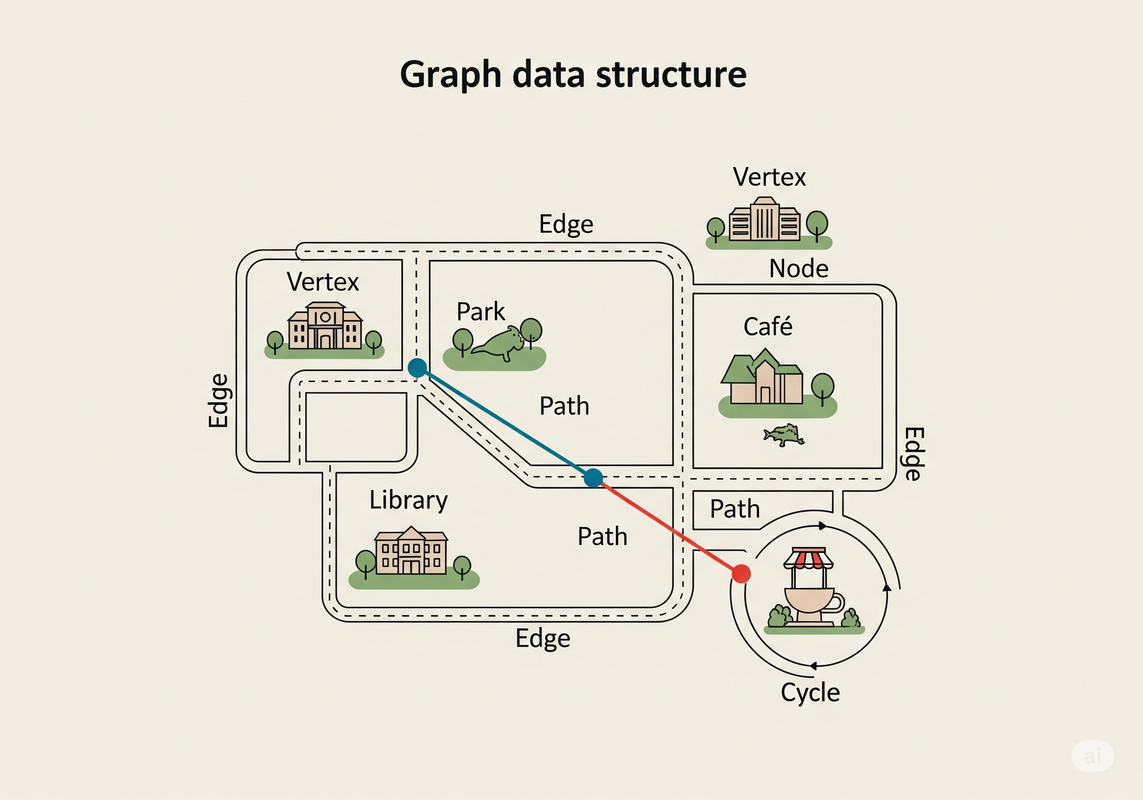
The key locations, landmarks, or intersections in the city are the vertices (or nodes) of the graph.
The roads, highways, or pathways connecting these locations are the edges.
Unlike a tree, graphs have no single root. You can start your journey at any vertex. There's also no strict parent-child relationship. Any vertex can be directly connected to any other. Crucially, graphs can have cycles, meaning you can start at one point, travel along edges, and return to your starting point (like driving around a city block).
3. The Language of Graphs: Key Terminology
Let's expand our vocabulary for navigating these networks.
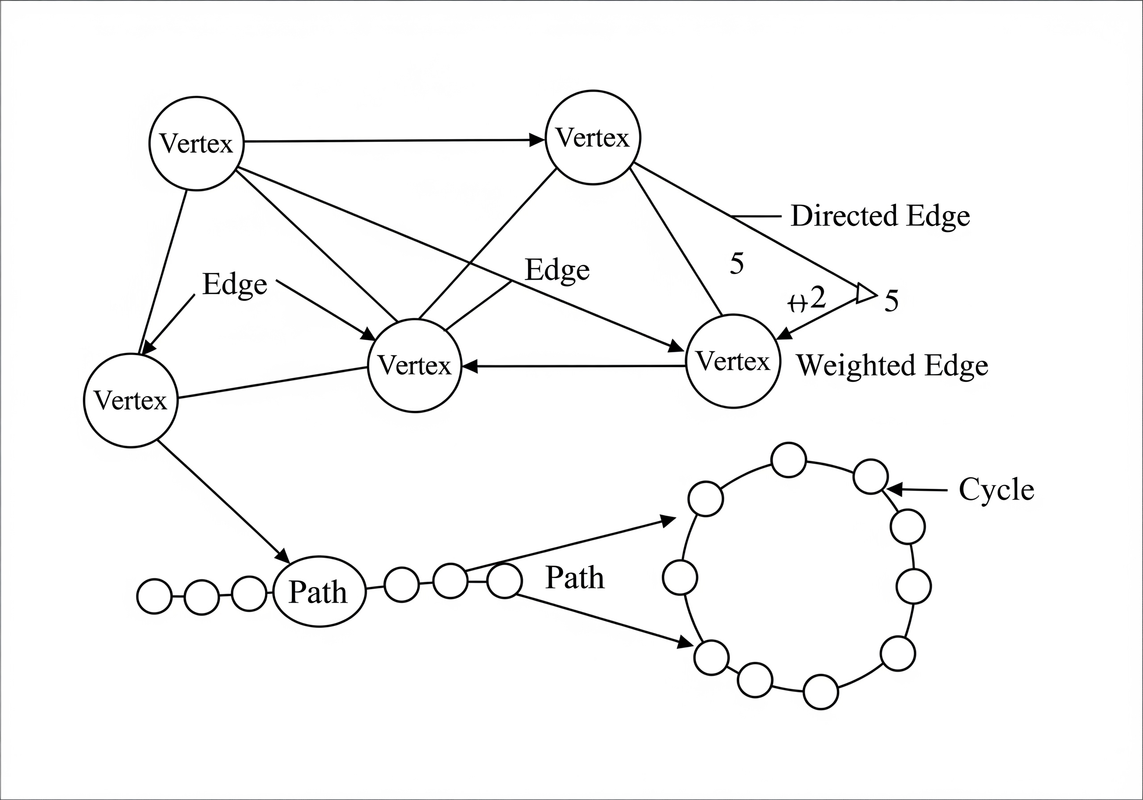
The Anatomy of a Graph: Vertices, Edges, and Their Properties.
- Vertex (plural: Vertices) / Node: A fundamental unit in a graph, representing an entity.
- Edge: A connection between two vertices, representing a relationship.
- Directed Edge: An edge with a specific direction, often represented by an arrow (e.g., a one-way street).
- Undirected Edge: An edge with no specific direction (e.g., a two-way road).
- Weighted Edge: An edge associated with a value or cost (e.g., the distance between two cities).
- Path: A sequence of vertices where each consecutive pair is connected by an edge.
- Cycle: A path that starts and ends at the same vertex.
- Adjacent Vertices: Two vertices are adjacent if they are connected by an edge.
- Degree of a Vertex (for undirected graphs): The number of edges connected to the vertex.
- In-degree (for directed graphs): The number of edges pointing to the vertex.
- Out-degree (for directed graphs): The number of edges pointing from the vertex.
- Isolated Vertex: A vertex with no incident edges.
- Simple Graph: A graph with no self-loops (edges connecting a vertex to itself) and no multiple edges between the same pair of vertices.
- Multigraph: A graph that allows multiple edges between the same pair of vertices.
4. Representing the Network: Adjacency Matrix vs. Adjacency List
To work with graphs in code, we need ways to represent their structure. The two most common methods each have their own advantages and disadvantages.
A. Adjacency Matrix: The Grid of Connections
An Adjacency Matrix is a 2D array (a grid) where both the rows and columns represent the vertices of the graph. The value at matrix[i][j] indicates whether there is an edge between vertex i and vertex j.
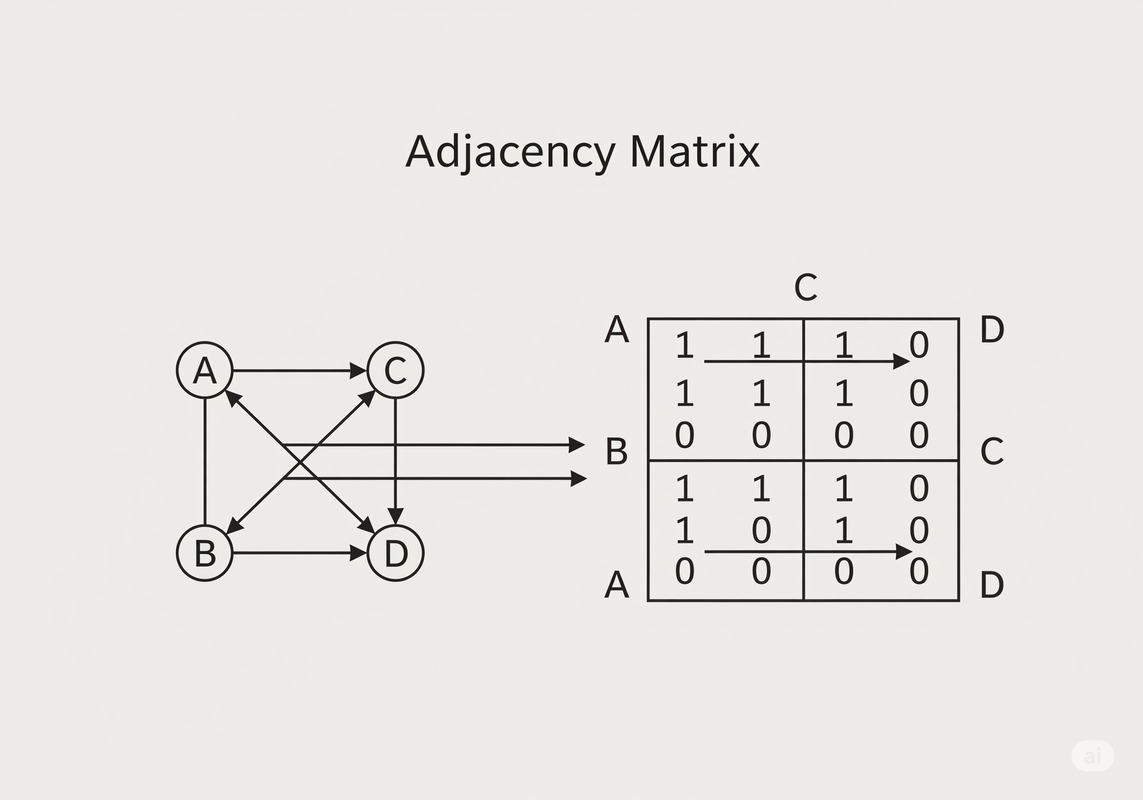
Adjacency Matrix: A grid representing direct connections.
B. Adjacency List: Neighbors at a Glance
An Adjacency List represents a graph as a collection of lists. For each vertex in the graph, there is a list that contains all the vertices that are directly adjacent to it (its neighbors).
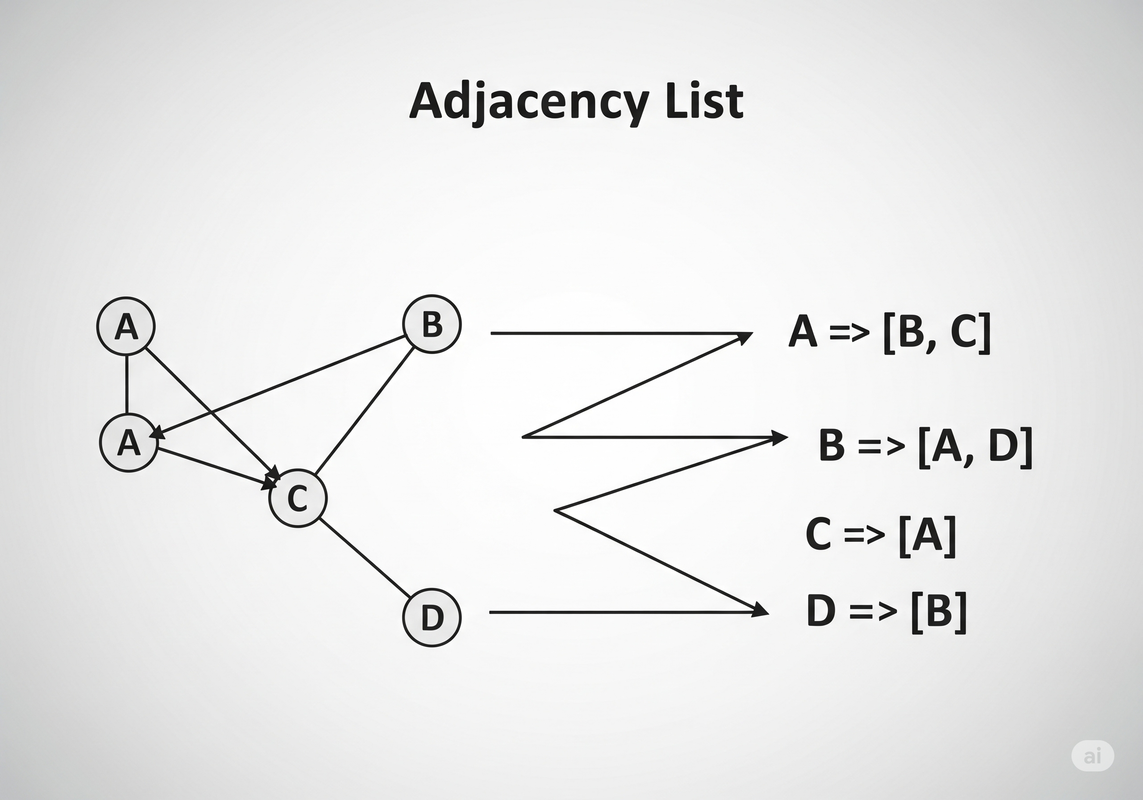
Adjacency List: A list of neighbors for each vertex.
5. Choosing Your Weapon: Matrix vs. List
The choice between Adjacency Matrix and Adjacency List depends on the specific problem and the characteristics of the graph.
| Feature | Adjacency Matrix | Adjacency List |
|---|---|---|
| Space Complexity | O(V²) | O(V+E) |
| Check edge (u, v) | O(1) | O(degree(u)) |
| Iterate all edges | O(V²) | O(V+E) |
| Good for... | Dense graphs | Sparse graphs |
6. Visualizing Traversal Algorithms
Navigating a graph requires a systematic approach to avoid getting lost in cycles. The two primary strategies are Depth-First Search (DFS) and Breadth-First Search (BFS). Use the interactive simulation below to see how each method explores the graph, highlights the currently executing line of code, and explains the logic at each step.
7. Blueprint Summary
Concepts Unlocked: Graphs, Vertices, Edges, Directed vs. Undirected Graphs, Weighted Edges, Paths, Cycles, Degree, In-degree, Out-degree, Isolated Vertices, Simple vs. Multigraph, Adjacency Matrix, Adjacency List.