Blueprint 9: "The Sorted Library" 📚

Blueprint 9: "The Sorted Library" 📚

Welcome, Architect. We've seen how trees can represent hierarchical data. But traversing an entire tree just to find one specific protocol is inefficient. The Labyrinth's ancient architects knew this, so they created a special, more organized type of tree that allows for high-speed searches by keeping itself sorted at all times. This structure is the Binary Search Tree (BST).

1. The Mission Briefing

Our mission is to achieve logarithmic search time, the gold standard for searching. A standard binary tree gives us no guarantees. To find an element, we might have to check every single node, resulting in a linear O(n) search time. We need a structure that is both hierarchical and ordered, combining the strengths of a tree with the speed of binary search. The BST is that design.

2. The Analogy: The Dictionary

A Binary Search Tree is like a very organized dictionary. For any given word (a node), all words that come before it alphabetically are on the left pages (the left subtree), and all words that come after it are on the right pages (the right subtree).

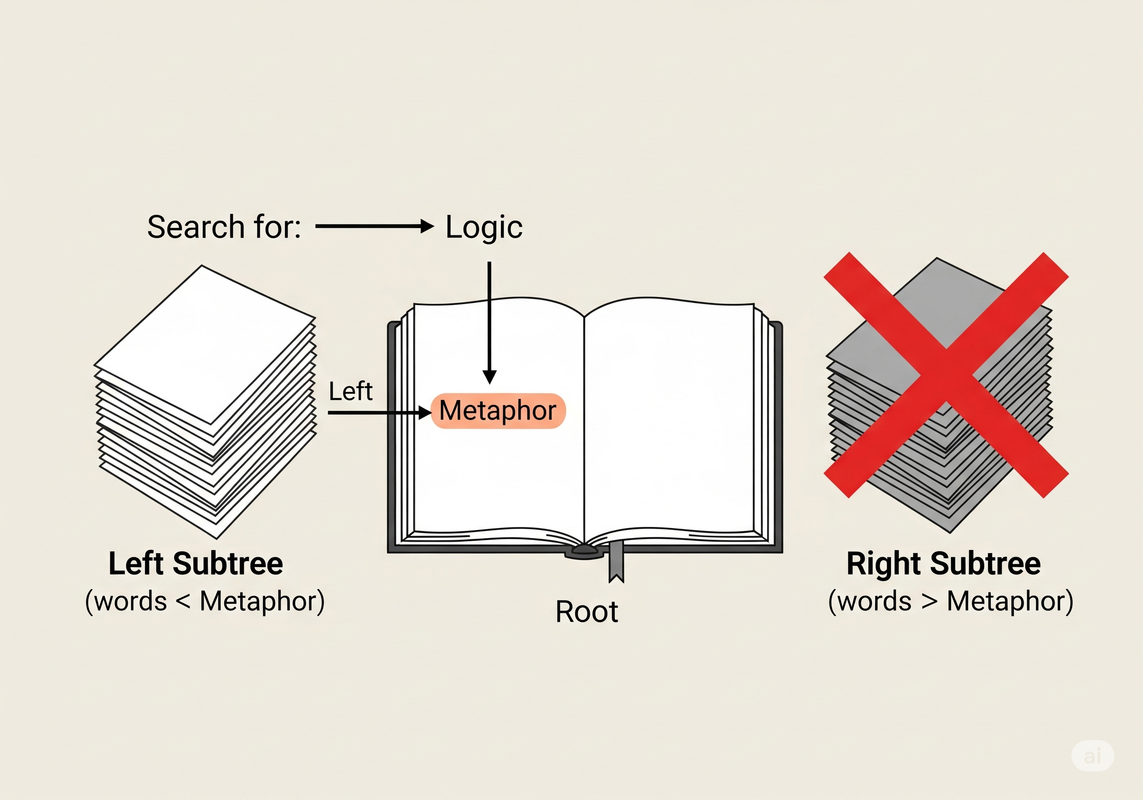
Imagine you are looking for the word "Logic". You open the dictionary to the middle, at "Metaphor". You know "Logic" comes before "Metaphor", so you instantly discard the entire right half of the dictionary and focus only on the left half. You repeat this process—opening to the middle of the remaining section and discarding half—until you zero in on your target word. A BST automates this exact process.

3. The Logic: The BST Property

A Binary Search Tree is defined by a single, powerful rule that must hold true for every single node in the tree:

The BST Property: For any given node N, all values in its left subtree must be less than N's value, and all values in its right subtree must be greater than N's value.

This simple rule is the key to its efficiency. At every node you visit, you can make a decision to go left or right, effectively pruning half of the remaining tree from your search space.

Core Operations: Building the Library

Understanding the property is one thing; implementing it is another. Let's explore the core operations for a BST. A tree node is typically a simple structure:

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

Searching a BST

This is the primary use case. The algorithm is a direct translation of the dictionary analogy.

1. Start at the root.
2. Compare the target value with the current node's value.
3. If they match, you've found the node!
4. If the target is less than the current node's value, move to the left child.
5. If the target is greater than the current node's value, move to the right child.
6. If you reach a null (empty) spot, the value does not exist in the tree.

The interactive simulation below demonstrates this efficient search process.

Inserting into a BST

To insert a new value, you first search for it. The search will eventually end at a null link where the node should be. You then insert the new node in that empty spot.

1. Start at the root.
2. Follow the search path (left for smaller, right for greater) as if you were looking for the new value.
3. When you would normally move to a null child, instead insert your new node in that position, linking it to its parent.

Deleting from a BST

Deletion is the most complex operation because you must ensure the BST property is maintained after the node is removed. There are three cases:

1. Case 1: Deleting a Leaf Node (No Children)
   This is the simplest case. You simply find the node and remove it by setting its parent's pointer to null.
2. Case 2: Deleting a Node with One Child
   This is also straightforward. You "bypass" the node by linking its parent directly to its child.
3. Case 3: Deleting a Node with Two Children
   This is the tricky one. You cannot simply remove the node, as that would break the tree into two disconnected subtrees. Instead:
   1. Find the node you want to delete.
   2. Find its in-order successor. This is the smallest value in the node's right subtree (go right once, then as far left as possible). The successor is guaranteed to have at most one right child.
   3. Copy the successor's value into the node you originally wanted to delete.
   4. Recursively delete the successor node from its original position (which will be an easier Case 1 or Case 2 deletion).

The Architect's Dilemma: The Problem of Balance

You've learned that BST search time is O(log n). But this comes with a huge catch. This ideal performance only happens if the tree is balanced. A balanced tree is one that is roughly as wide as it is tall, like a bushy, healthy tree.

What happens if you insert numbers into a BST in sorted order (e.g., 10, 20, 30, 40, 50)?

10
  \
   20
     \
      30
        \
         40
           \
            50
              

In the unbalanced tree, searching for a value is no different from searching in a linked list. You have to traverse the entire chain, making the search time degrade to the worst-case O(n).

This is the critical flaw of a simple BST. To solve this, master architects created Self-Balancing Binary Search Trees (like AVL Trees and Red-Black Trees). These special trees perform automatic "rotations" to maintain balance after every insertion and deletion, guaranteeing O(log n) performance. We will study these advanced blueprints later.

Traversing the Library: How to Read the Tree

Sometimes you need to visit every single node in the tree, for example, to print all the values. There are two main approaches: Depth-First and Breadth-First.

Depth-First Traversal (DFS)

This approach goes as deep as possible down one path before backtracking.

• In-order (Left, Root, Right): Visits the left child, then the root, then the right child.
  Special Property: In-order traversal of a BST visits the nodes in their sorted order. This is a fundamental and very useful property.
• Pre-order (Root, Left, Right): Visits the root first. Useful for creating a copy of the tree.
• Post-order (Left, Right, Root): Visits the root last. Useful for deleting nodes from a tree.

Breadth-First Traversal (BFS)

Also known as Level-Order Traversal, this approach explores the tree layer by layer, from top to bottom. It visits all nodes at depth 1, then all nodes at depth 2, and so on. This is typically implemented using a Queue data structure.

Architect's Log: Summary

• Binary Search Tree (BST): A binary tree that adheres to the BST Property: for any node N, left-subtree < N < right-subtree.
• Core Benefit: This property allows for logarithmic time complexity O(log n) on average for search, insert, and delete operations.
• The Catch: This performance is only achieved if the tree is balanced. A skewed, unbalanced tree degrades to O(n) performance.
• Operations: Search and Insert are straightforward extensions of the BST property. Delete is more complex, with three distinct cases to handle.
• Traversals: In-order traversal of a BST yields the elements in ascending sorted order, a key feature of this data structure.

The BST is a foundational "sorted library." While it has its flaws (the need for balance), understanding its structure is essential before moving on to more advanced, self-balancing tree structures.