Blueprint 2: "Understanding the Efficiency Rating" ⏱️

1. The Story: The Mission Briefing

"Excellent work, Architect. You found the beacon, but it took time. ALC Command measures every algorithm with an 'Efficiency Rating' based on Big O Notation. This rating tells us how an algorithm will perform under pressure. A low rating is the difference between life and death in a critical situation."

2. The Analogy: A Library of Cosmic Archives

Imagine you're in the Labyrinth's Grand Library, searching for a specific data-scroll (an item of data).

• O(n) Linear Time: The scrolls are in a jumbled pile. You have to look through them one by one. If the pile has 100 scrolls, it might take you 100 checks. If it has a million, it might take a million checks. The time taken grows in a straight line with the number of items (n). This was your last mission.
• O(1) Constant Time: You ask the librarian, and they know *exactly* where the scroll is. It doesn't matter if there are 10 scrolls or 10 billion, the time to get it is the same. This is the holy grail of efficiency, like accessing an array by its index.
• O(log n) Logarithmic Time: The scrolls are sorted alphabetically. You open the book to the middle. If your scroll comes before, you ignore the entire second half. If it comes after, you ignore the first half. You repeat this, halving the search area each time. This is incredibly fast for large collections. A million scrolls takes only about 20 checks!

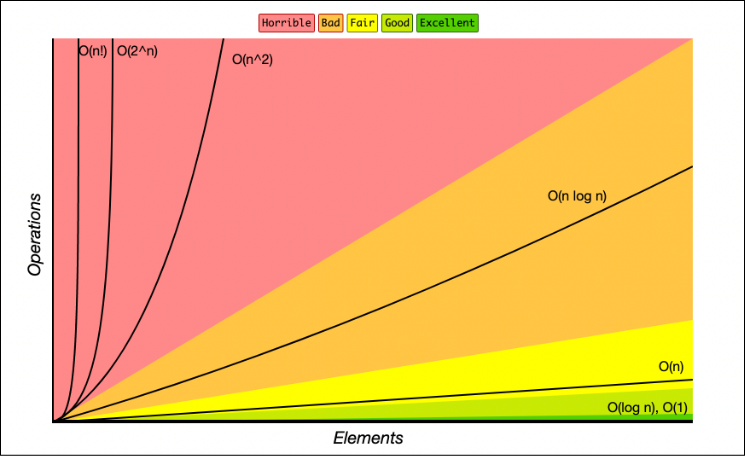
3. The Logic: Visualizing Growth

Big O describes the worst-case scenario and focuses on how the number of operations grows relative to the input size (n). We ignore constant factors (like "is my computer twice as fast?") and focus on the shape of the growth curve. As an Architect, your goal is to always choose the algorithm with the flattest possible growth curve for the task at hand, especially when dealing with large amounts of data.

A Concrete Example: Primality Testing

Let's say you need to check if a large number, N, is prime.

• The Naive O(n) Approach: You could check for divisibility by every single number from 2 all the way up to N-1. If you find any divisor, the number is not prime. For a number like 1,000,000,007 (which is prime), this would take over a billion operations. Far too slow!
• The Optimized O(√n) Approach: A mathematical insight reveals that if a number N has a divisor larger than its square root, it must also have a corresponding divisor that is *smaller* than its square root. Therefore, you only need to check for divisors up to √N. For 1,000,000,007, the square root is about 31,622. This is a monumental improvement. Instead of a billion operations, you only need about thirty thousand. This is the difference between a mission-critical system that responds instantly and one that fails under pressure.

4. Concepts Unlocked