Blueprint 13: "Exploring the Solution Maze" 🗺️

Blueprint 13: "Exploring the Solution Maze" 🗺️

1. The Mission Briefing: When Simple Choices Aren't Enough

"Architect, not all problems can be solved with a simple greedy choice. Some, like cracking a combinatorial lock, require you to explore many different paths. If a path leads to a dead end, you must be able to go back and try another. This is the Backtracking paradigm."

We've seen how Greedy algorithms make locally optimal choices. But what if the best immediate step leads us down a path from which we can never recover the optimal solution? For problems that involve exploring a vast number of possibilities, where the consequences of a choice aren't immediately clear, we need a more systematic approach. This is where Backtracking comes into play.

2. The Analogy: Solving a Maze

A perfect analogy for backtracking is a group of explorers charting a new cave system. They stand at an intersection with three tunnels.

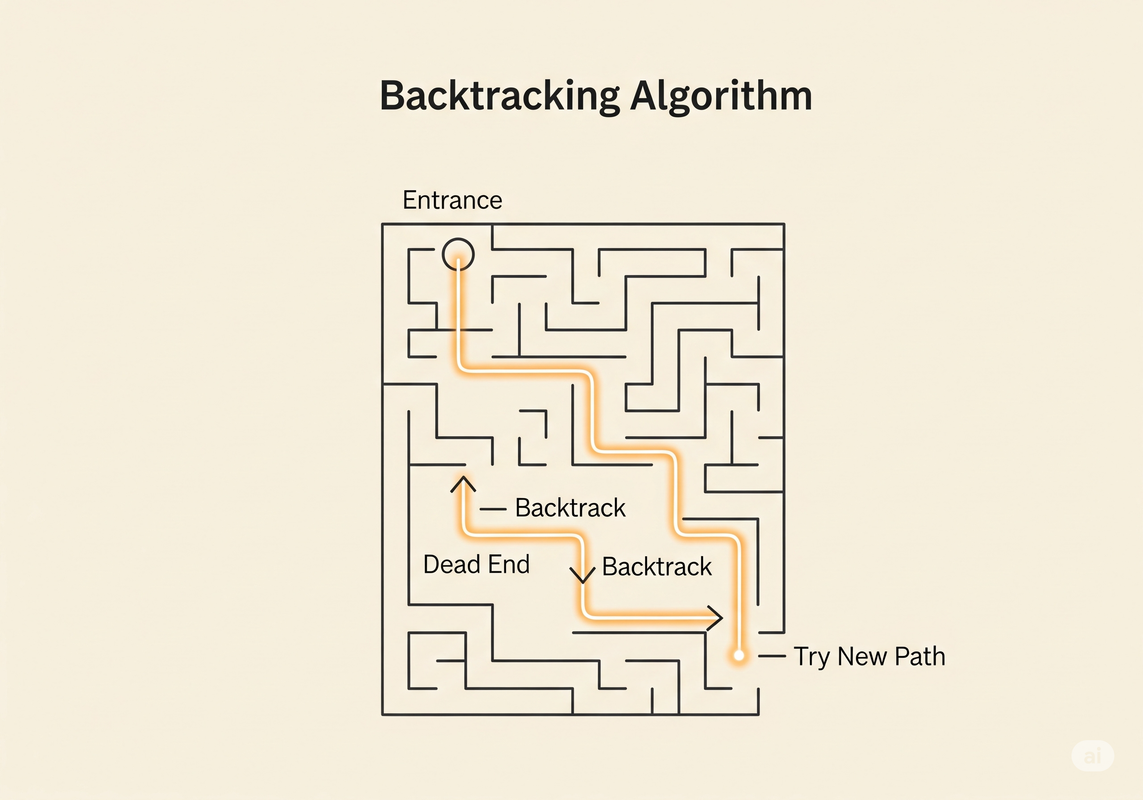
The team doesn't know which tunnel leads to the exit. So, they systematically explore:

1. Choose: The lead explorer decides to try the first tunnel.
2. Explore: The team walks down the tunnel, marking their path so they know they've been there.
3. Hit a Dead End: The tunnel leads nowhere. The path is invalid.
4. Unchoose (Backtrack): The team retraces their steps back to the original intersection.
5. Choose Again: Now at the intersection, they know the first tunnel is a bust. They choose the second tunnel and repeat the process.

This is the essence of backtracking: exploring a path, and if it fails, returning to the last choice point to try a different option.

3. The Core Concepts: State Space and Exploration

Backtracking operates within the concept of a state space.

• State: A particular configuration of the problem (e.g., your current location in the maze, the current arrangement of numbers in a Sudoku puzzle).
• State Space: The set of all possible states the problem can be in. Our goal is to find a goal state (e.g., reaching the exit of the maze, a complete and valid Sudoku solution).

Backtracking explores this state space using a depth-first search (DFS) approach. It tries to go as deep as possible down one path before exploring other possibilities.

4. The Recursive Engine: How Backtracking Works

Backtracking is often implemented using recursion due to its natural way of representing the "go forward" and "come back" steps. A typical backtracking algorithm follows these steps:

1. Choose: Make a choice that leads to a new state.
2. Explore: Recursively explore the state space from this new state.
3. Unchoose (Backtrack): If the exploration from the new state doesn't lead to a solution, undo the choice you made in step 1 and try a different choice.

The recursive flow of a backtracking algorithm: Choose, Explore, Unchoose.

5. Visualizing Backtracking in Action

Let's use the maze analogy to visualize the backtracking process.

6. The Architect's Toolkit: Key Backtracking Techniques

While the core idea is simple, effective backtracking often involves these strategies:

• Constraint Satisfaction: Before exploring a new state, check if it violates any constraints of the problem. If it does, prune that path early to avoid unnecessary exploration.
• Pruning: Intelligently cutting off branches of the search space that are guaranteed not to lead to a solution. This can significantly improve efficiency.
• Maintaining State: Keep track of the current state of the solution being built (e.g., the numbers placed in a Sudoku grid so far, the path taken in a maze).
• Base Cases: In a recursive backtracking function, clearly define the base cases that indicate either a solution has been found or a dead end has been reached.

7. Classic Backtracking Problems

Backtracking is a powerful technique for solving a wide range of combinatorial problems:

• N-Queens Problem: Placing N non-attacking queens on an N×N chessboard.
• Sudoku Solver: Filling a 9x9 grid with digits so that each column, each row, and each of the nine 3x3 subgrids contains all of the digits from 1 to 9.
• Permutations: Generating all possible orderings of a set of elements.
• Combinations: Generating all possible subsets of a given size from a set of elements.
• Graph Coloring: Assigning colors to the vertices of a graph such that no two adjacent vertices share the same color.
• Word Search: Finding if a given word exists in a grid of letters.

8. Code Example: Generating Permutations

Here's a classic example of backtracking used to generate all permutations of an array.

def permute(nums):
    result = []
    
    def backtrack(start_index):
        if start_index == len(nums):
            result.append(list(nums))
            return
        
        for i in range(start_index, len(nums)):
            # Choose: Swap the current element with the start element
            nums[start_index], nums[i] = nums[i], nums[start_index]
            # Explore
            backtrack(start_index + 1)
            # Un-choose: Swap back to restore the original state
            nums[start_index], nums[i] = nums[i], nums[start_index]

    backtrack(0)
    return result

9. Blueprint Summary

Concepts Unlocked: Backtracking, State-Space Search, Recursive Exploration, Constraint Satisfaction, Pruning, Maintaining State, Base Cases.