Blueprint 12: "The Locally Optimal Choice" 💰

1. The Story: The Mission Briefing

"Architect, some of the Labyrinth's most complex optimization problems have a surprisingly simple solution. The Greedy paradigm teaches us that sometimes, making the best possible choice at the current moment, without worrying about the future, can lead to the best overall outcome."

While some problems require complex, forward-thinking strategies like Dynamic Programming, others can be conquered with a more straightforward approach. A Greedy algorithm builds a solution piece by piece, and at each step, it makes the choice that seems the best right now. The hope is that a series of these locally optimal choices will lead to a globally optimal solution.

2. The Analogy: Giving Change

If you need to give someone 48 cents in change, you don't plan out every possible combination of coins. Your brain instinctively uses a greedy approach:

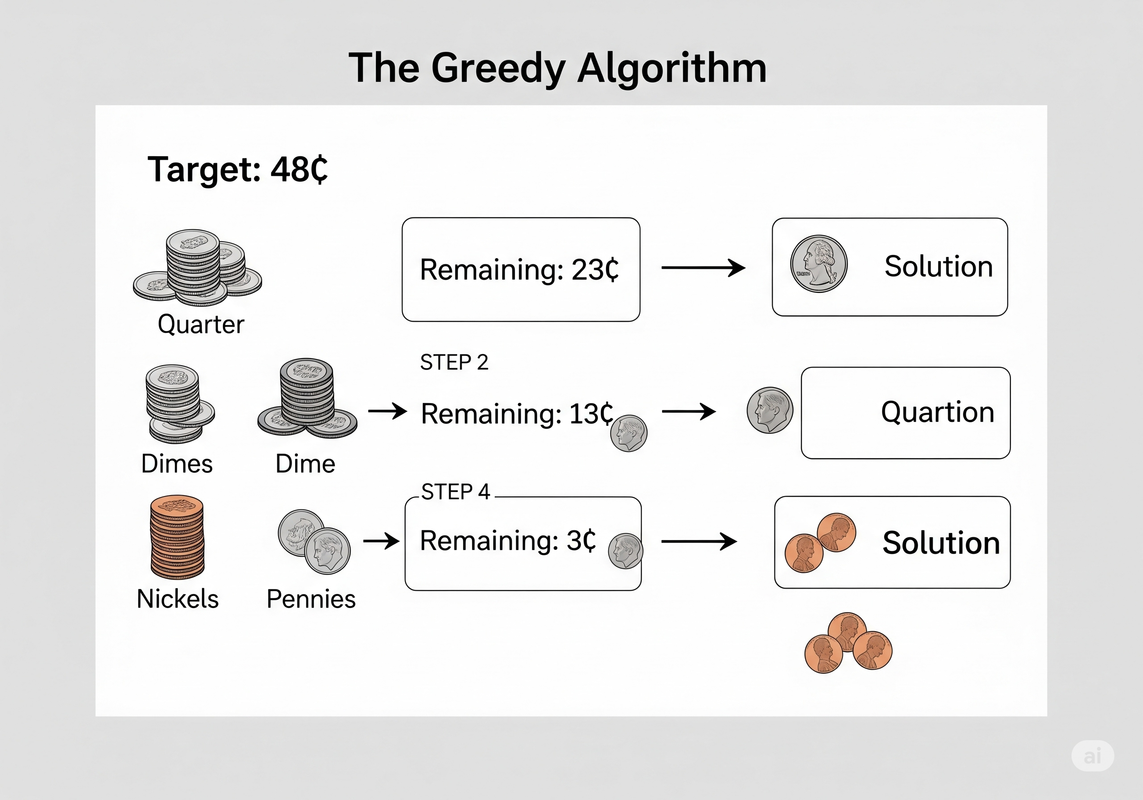
1. What's the biggest coin I can use? A quarter (25¢). Now I owe 23¢.
2. What's the biggest coin for 23¢? A dime (10¢). Now I owe 13¢.
3. What's the biggest coin for 13¢? Another dime (10¢). Now I owe 3¢.
4. What's the biggest coin for 3¢? A penny (1¢). Then another, and another.

For standard currency, this simple "greedy" choice at each step results in the fewest possible coins. This approach doesn't work for all problems, but when it does, it's often the simplest and fastest.

3. The Architect's Dilemma: When Can We Be Greedy?

The "Giving Change" analogy works perfectly for standard US coins, but what if the available coins were {1, 7, and 10} cents, and you needed to make 15 cents?

• The greedy choice would be: 10 + 1 + 1 + 1 + 1 (5 coins).
• The optimal solution is: 7 + 7 + 1 (3 coins).

This proves that a greedy approach is not always optimal. A problem must have two special properties for a greedy algorithm to be guaranteed to work:

• Greedy Choice Property: This means that a globally optimal solution can be arrived at by making a locally optimal choice. We never have to go back and reconsider our choice.
• Optimal Substructure: This means that an optimal solution to the overall problem contains the optimal solutions to its subproblems. The optimal way to make change for 48 cents (a quarter + an optimal solution for 23 cents) contains the optimal solution for making change for 23 cents.

4. Code Example: Change-Making Algorithm

Here is a simple implementation of the greedy change-making algorithm for standard currency.

def find_min_coins(amount: int) -> list[int]:
    coins = [25, 10, 5, 1]  # Sorted denominations
    result = []
    
    for coin in coins:
        while amount >= coin:
            result.append(coin)
            amount -= coin
            
    return result

5. Classic Greedy Scenarios

The greedy paradigm is used to solve many famous problems:

• The Fractional Knapsack Problem: To maximize profit, you greedily take as much of the most valuable material (highest value-per-kilogram) as you can, then the next most valuable, and so on.
• Activity Selection Problem: To schedule the maximum number of non-overlapping activities, you greedily select the activity that finishes earliest first.
• Huffman Coding: A famous data compression algorithm that uses a greedy approach to build an optimal prefix-free code for a set of characters.

6. Blueprint Summary

Concepts Unlocked: Greedy Algorithms, Local vs. Global Optimum, Greedy Choice Property, Optimal Substructure, and a brief comparison to Dynamic Programming.